SP#7: Unit Q Concept 2: Finding All Trig Functions when given one Trig Function and Quadrant ( Using Identities)

This SP7 was made in collaboration with Christine N. Please visit her awesome posts on her blog by going here.

I/D #3 Unit Q -Pythagoreom Identities

Inquiry Activity Summary

1)Well first off it is an identity. An identity is a proven fact or formula. The Pythagorean Theorem is an identity because it is a proven fact and forumla. Using x y and r we can see in letter b how the the Pythagorean theorem is written. Next we make the eaution eqaul to one by dividing by r^2 which leaves us with our final answer as seen in letter c. when we have it rewritten we see that x/r is a ratio for cosine on the unit circle and y/r is a ratio for sine on the unit circle. From this we can see how the unit circle plays into it.And from this information we conclude that cosine^2+sine^2=1. We add the sqaure because we can power these up.It is referred to as the pythagoreon identity because its just the theorem moved around a little. In letter h i chose 60 from the unit circle to prove that the identity is true.

2) In number two we have todervie the two remaining using what we came up with in letter f.In letter a i divided everything by cosine and what i was left with simplified to tan^2+1=sec^2 because what we had originally could be substituted using our identities. In b i did the same thing except this time i divided by sin^2.

Inquiry Activity Refelction

The connections that I see between Units N, O, P, and Q so far are that the unit circle comes into play alot of the time. From unit p we learned the basics of the traingles and how to find sides and angles and now we have taken it a step further with learning the law of sines and cosines. Also when we first learned how to graph angles in degrees and radians we use that for our word problems now.

If I had to describe trigonometry in THREE words, they would be difficult, puzzling, and usefull.

WPP #13- #14 Unit P Concept 6/7-One Post

Please see my WPP 13-14, made in collaboration with Vivian Pham, by visiting there blog here Also be sure to check out her other cool blog posts.

BQ:#1:Unit P

BIG QUESTIONS!

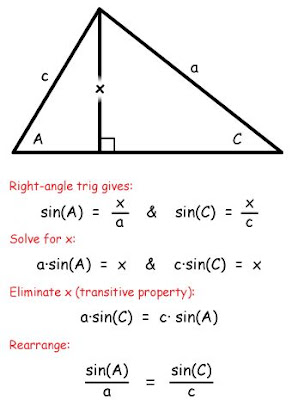
i. Law of Sines

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiACyal4Sb8T5jyRkmCPbk-qx4z2jLUyZS_GUMdSAmq8L2KuTaHNozh28CQyU5mlKiCyLnBwBEtaH9eFrBH1DOeKcocbn65RK7RVzFuMM06Mz_sySjlvD5ra0POAwfNDmjCfUS7otnmolg/s400/Law+of+sines+derivation.JPG

We need the Law Of Sines because sometimes we aren't working with traingles that are NOT right traingles, that is no 90 degree angle. Normal Trig functions are defined for a right triangle and are not directly useful in solving non-right triangles. However, even though we do not know we can use our handy dandy math skills to figure out the law of sines.

The picture below will demonstrate how to derive the law of sines. On the bottom it says LAW OF SINES IS THEN SIN A/a = SINB/b =SIN C/c !:)

iv. Area Formulas

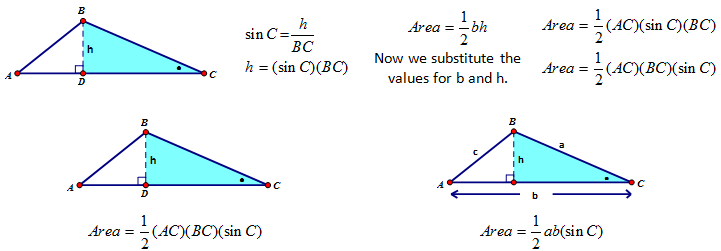http://www.geometrycommoncore.com/content/unit2/gsrt9/images/notes3.png

An oblique triangle is a triangle that has all side lengths that are different. To find the area of a triangle we know that its A=1/2BH. However, since the traingle is NOT a right traingle it has no H. If we draw a line representing H(height) and we can use what we know about traingles, such as SINE and the angles and sides we know to find H. In the triangle given above we know that SIN C = h /a . To get H alone we cross multiply to get the eqaution SIN C (a) =h. Now we H so we can sunstitute it back into our original Area Formula of A=1/2BH we get A= 1/2b(asinc). Notice that this formula requires no provided value for the height, the height is being calculated using the sine ratio. CALCULATING AREA THEN REQUIRES TWO SIDES OF A TRAINGLE AND THE INCLUDED ANGEL. SIDE ANGLE SIDE! (SAS)

Resources :)

http://www.geometrycommoncore.com/content/unit2/gsrt9/images/notes3.png

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiACyal4Sb8T5jyRkmCPbk-qx4z2jLUyZS_GUMdSAmq8L2KuTaHNozh28CQyU5mlKiCyLnBwBEtaH9eFrBH1DOeKcocbn65RK7RVzFuMM06Mz_sySjlvD5ra0POAwfNDmjCfUS7otnmolg/s400/Law+of+sines+derivation.JPG

WPP#12 Unit:O Concept:10

PROBLEM:Mammoth Mountain Running Camp

A)Segerstrom Cross country team heads over to Mammoth lakes over summer for elevation training. On the first day they do a run called the rock which is 1180 feet up vertically. They stand from the bottom up to the top of the mountain  at angle of 37 degrees. how long up is the trail? 

B) After they arrive at the top of the mountain they look down at an angle of depression of 16 degrees to a houses 3000 feet down vertically. How long is the trail now?

PICTURE:Mammoth Mountain Running Camp

http://www.liftopia.com/ski-resort-info/images/full/619002_logo_1384823487.jpg

Solution:Mammoth Mountain Running Camp

Sources:

http://www.liftopia.com/ski-resort-info/images/full/619002_logo_1384823487.jpg

I/D #2 Unit O-How can we derive the patterns for our special right triangles?

Inquiry Activity Summary

45-45-90 Triangle

First, I cut the square diagonally. I labeled all the angles 90 and the ones who got cut in half 45. 

They all add up to 360 like a square should.Each side length is 1 so we label each side one. ( Step one 

Picture) The diagonal side we don't know yet but since we know two sides are one as stated in the 

directions, we can figure out the diagonal side by using the pythagorean theorem, a^2 + b^2 = c^2. so 

its 1+1=c^2 so then c=sqaureroot 2. (Step two picture) Why "n"? In the sss packet we were given a 45-

45-90 triangle with side lengths of n,n, and n rad 2. Why is that? N is being used as a variable so that it 

can work in all problems with different types of numbers. In this example to get n,n, and nrad2, i just 

multiplied each by n.(Step 3 picture)

30-60-90 Triangle

First , I cut the equilateral triangle straight down the middle. Then I labeled each side and angle 

according to what i was given. Since each side was one and the bottom got cut in half, it is now 1/2. 

We now know 2 sides. One side is 1/2 and one side is 1. We can use the Pythagorean Theorem to 

figure it out but this time we know a and c and are looking for b. (Math work on picture)Finally since 

we now know b is  rad 3/2 and a is 1/2 and c is 1 we need to derive them so that they corresponds to 

all numbers. So what i did was i multiplied each one by 2n. A which was 1/2 became n, b which was 1 

became 2n, and c which was rad 3/2 became n rad 3. (Math work shown on picture). The reason why 

we need to have n is because not all problems will have 1 as the numbers, it has to be able to work for 

all numbers so n acts as the variable.

Inquiry Activity Reflection

Something I never notcied before about special right traingles are that they actaully originate from something. I didn't know that the 45-45-90 came from a sqaure or that the 30-60-90 came from another traingle. I thought that these triangles were just traingles.

Being able to derive these patterns myself aids in my learning beacuse once I know how to get the varaibles that go with these traingles, solving for the sides will be easier now that I know how to get them in the first place. Solving these traingles is no longer just memorization but application of math.