BQ#7 Unit V

Picture Discription of how to get the slope of the secant line

To start of basically you have a secan line drawn, that means it touches two points on the graph. The first distance you have is the (x ) and the one next to it is the (h ). the vertical up to point a is f of x f(x) and then the distance up is f (x+h) because it has to go the disatnce of x and h. The cordinates of a is (x , f(x) ) and of b its ( (x+h) , f(x+h) ).

The math of how to get the difference quotient!

To find how those points and how its revelent, we have to use the slope formula. Since we are finding the slope we can find the slope to help find the difference qoutient. In the end we just cancel out things and we are left with our famous f(x+h)-f(x)/h!!!!!!!

MINDBLOWN!

BQ#6 : UNIT U

1. What is continuity? What is discontinuity?

A continuous function means you can draw it without your pencil lifting from the paper. It is predicatble meaning you know whats going to happen. There are no breaks, jumps, or holes. It can be drawn with a single unbroken pencil stroke.  ex: lim as x approaches c of f(x)=f(c)- the limit and value are the same. On the other hand a discontinuous function is UNpredicatble. There are 4 types of discontinuities. A point discontinuity, which is also known as a hole, a jump discontinuity(different left and right ), oscillating behavior (wiggly), and an infinite discontinuity which results in unbounded behavior caused by a vertical asymptote. These continuities from two families, non removable, and removable discontinuities.

2.What is a limit? When does a limit exist? when does a limit not exist? What is the difference between a limit and a value?
A limit is the intended height of the function. A limit exists as long as you reach the same height from the left and the right. A limit does NOT exist if the right and left do not meet.

In the above picture the limit DOES exist because from both the left and right it approaches the same intended height.

In the above picture the limit DOES not exist because of a jump discontinuity and also because the left and right do NOT reach the same intended height.

A limit is the intended height, which means it can or cannot reach it, and the value is the ACTUAL height, or what it reaches.

3.How do we evaluate limits numerically, graphically, and algebraically?
To evaluate limits algebraically you can use three " shortcut" ways. There is the direct substitution way which is basically plugging in the x into the function. When doing this method you can produce 1 of 4 answers. You can get a numerical answer which means you are done. You can get a 0/# answer which means you are done. You can get a #/0(undefined) and you are done. Finally you can get 0/0, or indterminate form which requires more work. If the first method does not work you may use the dividing out/ factoring method. In this case you factor out the numerator and denominator and cancel out common terms to remove zero in the denominator. Then , use direct substitution with the simplified expression. Lastly, there is the rationalizing/conjugate method. If it is a fraction , then multiplying the top and bottom by a conjugate would have helped. The conjugate is where you change the sign in the middle of the term. You use the conjugate of wherever the radical is.
To evaluate a limit graphically we look at the graph and from the left and right with our fingers you trace the limit. This means it has to be the same from the left and the right. Make sure to identify the discontinuities.
To evaluate the limit numerically you use tables. The limit as x will go in the middle box and then from the leftb and right the numbers get closer and closer then on the bottom you graph the function and hit trace on those values.

BQ #3 Unit T Concepts 1-3

How do graphs of sine and cosine relate to each of the others ? Emphasize asymptotes in your response.

Tangent?

Cotangent?

Secant?

Cosecant?

Cosecant

Cosecant is similar to sine.The ratio for cosecant is 1/sin and since sin is y/r cosecant is r/y.In the unit circle wherever sine is positive so is cosecant. So basically, since sin is positive so is cosecant in the first quadrant. Sine does not have any asymptotes because they only occur when there is an undefined answer. However, cosecant does have asymptotes at o and pi.

Secant 

Secant is related to cosine. Acording to the unit circle cosine is poitive in the first last quadrants and negative in the second and third. Secant follows this as well. The asymptotes or where an undefined answer occurs are at pi over 2  and 3pi over 2. This is where cosine is 0, making the ratio undefined. Because secant is 1/cosine. 

Cotangent

 The identity for cotangent is cosine over sine or x/y. It is very similar to tangent. Cosine and sine are positive in the first quadrant because cosine/sine will be positive In the second quadrant, the sine is positive and cosine is negative, so cotangent is negative because a negative cosine divided by a positive(sign wise) will be negative. For the third quadrant, cosine and sine are negative, making cotangent positive because a negative divided by a neagtive will cancel out the signs and make the answer positive. In the last quadrant cosine isnpositive and sine is negative, making cotangent negative because, again, a neagtive and positive leaves a negative. Since asymptotes occur when 0 is below the divid]sion sine, sine must eqaul zero so that an undefined answer may occur and asymptotes are found. Therefore, we know that sine is equal to 0at 0 and pi. 

Tangent
The identity for tangent is sine/cosine or y/x.  If sine or cosine are negative, then tangent will be negative because a negative and positive sign make a negative answer. If sine or cosine are positive or  both negative, tangent will be positive because a negative and negative sign will be positive, as they cancel out. In the first quadrant, sine and cosine are positive, so tangent is positive. In the second quadrant, cosine is negative, but sine is positive so it is negative.In the third quadrant, both sine and cosine are negative, making tangent positive as they both cancel out each others signs. The fourth quadrant is negative because cosine is positive, but sine is negative. Tangent has asymptotes when cosine is equal to 0 because cosine in the denominator. They are at pi/2 and 3pi/2

BQ # 5 Unit T Concepts 1-3

BQ #5

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

Asymptotes only occur when it is undefined. What that means is the answer from a trig ration product has to be undefined. Zero must be in the denominator. The trig ratio for sine is y/r , cosine is x/r , cosecant is r/y , secant is r/x , tangent is y/x , cotangent is x/y. ZERO HAS TO BE IN THE DENOMINATOR FOR THE ANSWER TO BE UNDEFINED. the only trig functions that produce a undefined answer are all but sine and cosine. Sine is y/r and r=1 therfore there cannot be an undefined answer. Cosine is x/r and r=1, again it cannot be undefined. Cosecant is r/y and y can be 0 on a certian place on the unit circle so it can be defined. The same for secant with x in the bottom. Tangent with x in the bottom and cotangent with y in the bottom.

BQ #4 Unit T: Concept 3

Why is a “normal” tangent graph uphill, but a “normal” tangent graph downhill? Use unit circle ratios to explain.

To start off, tangent and cotangent graphs have asymptotes. The graph cannot touch the asymptotes. To have asymptotes sin has to be 0 so that it is undefined and cosine has to eqaul 0 so that tangent is undefined. In the examples shown below the period must occur between then asymptotes and CAN'T TOUCH IT. Beacuse the asymptotes are in different marks, tangent being at 90 and 270 and cotangent being at 180 and 360, in order for the graph to not touch the asymptote, tangent must go up and cotangent must go down.

BQ #2 Concept:intro

BQ #2 !!!!!!!!!!!!!!!

First question

First off, a period is how long it takes for a pattern to occur fully in. For sine quadrant 1 is positive, quadrant 2 is positive, qaudrant 3 is negative, and quadrant 4 is negative. Therefore, the pattern is + - + - . Since it takes the whole unit circle to complete this pattern it takes 2pie. For cosine qaudrant 1 is positive , 2 is negative, 3 is negative, and 4 is positive. So the pattern that occurs is + - - + . Again for the pattern to repeat , since there is no repeating unit like sine, it is 2pie. The first qaudrant of tangent is positive the second negative the third positive and the 4th negative. The pattern in + - + - . They pair + - repeats twice so the period is pie because it takes pie units to complete the cycle.

Question #2 
Amplitudes are half the distance between the highest and lowest points on the graph. Sine and Cosine graphs have these. Amplitudes are like restrictions. When taking the sine or cosine inverse , the number for these two trig identies are between -1 and 1 because they take the x/r and y/r. The other trig identies dont have restrictions at all and thats why they dont have amplitudes.

Reflection#1: Unit Q Verifying Trig Identies

1. It just meas to break it apart. Essentially that is what you are doing. They both mean the same thing in the end. There are different ways of doing it. Verifying is not done by some specific way. There are so many different thought processes to do it. Some take a lot of time while othere take minimal time. Pay careful attenton to your work. Memorize the identities.
2. Memorize!!!!!!!! Once you memorize the trig functions, everything else comes together. When your stuck just convery everything to sin and cos that helps. Take everything apart step by step. Another trick that is helpful is to multiply by the conjugate when its a fraction and you don"t know what to do. NEVER divide by an identiy. Most likley when you have the urge to do that just multiply by the conjugate. Verifying is the easiest because you already know the answer, all you need to do is find a way there. Try different identities. Break it apart.
3. When i first look at a problem the first thing I think of is sin and cos. They are easiest to deal with when they are in sin and cos. HOWEVER, always check if theres an identity there. For example any of the pythagoreom theroems can be hidden etc. Next i hope that things start to cancel or if there is a fraction multiply by conjugate. Most likley if things get messier you are not doing it right. I feel like most of it is trial and error. You plug and chug and eventually you get yur answer. Patience is key

SP#7: Unit Q Concept 2: Finding All Trig Functions when given one Trig Function and Quadrant ( Using Identities)

This SP7 was made in collaboration with Christine N. Please visit her awesome posts on her blog by going here.

I/D #3 Unit Q -Pythagoreom Identities

Inquiry Activity Summary

1)Well first off it is an identity. An identity is a proven fact or formula. The Pythagorean Theorem is an identity because it is a proven fact and forumla. Using x y and r we can see in letter b how the the Pythagorean theorem is written. Next we make the eaution eqaul to one by dividing by r^2 which leaves us with our final answer as seen in letter c. when we have it rewritten we see that x/r is a ratio for cosine on the unit circle and y/r is a ratio for sine on the unit circle. From this we can see how the unit circle plays into it.And from this information we conclude that cosine^2+sine^2=1. We add the sqaure because we can power these up.It is referred to as the pythagoreon identity because its just the theorem moved around a little. In letter h i chose 60 from the unit circle to prove that the identity is true.

2) In number two we have todervie the two remaining using what we came up with in letter f.In letter a i divided everything by cosine and what i was left with simplified to tan^2+1=sec^2 because what we had originally could be substituted using our identities. In b i did the same thing except this time i divided by sin^2.

Inquiry Activity Refelction

The connections that I see between Units N, O, P, and Q so far are that the unit circle comes into play alot of the time. From unit p we learned the basics of the traingles and how to find sides and angles and now we have taken it a step further with learning the law of sines and cosines. Also when we first learned how to graph angles in degrees and radians we use that for our word problems now.

If I had to describe trigonometry in THREE words, they would be difficult, puzzling, and usefull.

WPP #13- #14 Unit P Concept 6/7-One Post

Please see my WPP 13-14, made in collaboration with Vivian Pham, by visiting there blog here Also be sure to check out her other cool blog posts.

BQ:#1:Unit P

BIG QUESTIONS!

i. Law of Sines

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiACyal4Sb8T5jyRkmCPbk-qx4z2jLUyZS_GUMdSAmq8L2KuTaHNozh28CQyU5mlKiCyLnBwBEtaH9eFrBH1DOeKcocbn65RK7RVzFuMM06Mz_sySjlvD5ra0POAwfNDmjCfUS7otnmolg/s400/Law+of+sines+derivation.JPG

We need the Law Of Sines because sometimes we aren't working with traingles that are NOT right traingles, that is no 90 degree angle. Normal Trig functions are defined for a right triangle and are not directly useful in solving non-right triangles. However, even though we do not know we can use our handy dandy math skills to figure out the law of sines.

The picture below will demonstrate how to derive the law of sines. On the bottom it says LAW OF SINES IS THEN SIN A/a = SINB/b =SIN C/c !:)

iv. Area Formulas

http://www.geometrycommoncore.com/content/unit2/gsrt9/images/notes3.png

An oblique triangle is a triangle that has all side lengths that are different. To find the area of a triangle we know that its A=1/2BH. However, since the traingle is NOT a right traingle it has no H. If we draw a line representing H(height) and we can use what we know about traingles, such as SINE and the angles and sides we know to find H. In the triangle given above we know that SIN C = h /a . To get H alone we cross multiply to get the eqaution SIN C (a) =h. Now we H so we can sunstitute it back into our original Area Formula of A=1/2BH we get A= 1/2b(asinc). Notice that this formula requires no provided value for the height, the height is being calculated using the sine ratio. CALCULATING AREA THEN REQUIRES TWO SIDES OF A TRAINGLE AND THE INCLUDED ANGEL. SIDE ANGLE SIDE! (SAS)

Resources :)

http://www.geometrycommoncore.com/content/unit2/gsrt9/images/notes3.png

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiACyal4Sb8T5jyRkmCPbk-qx4z2jLUyZS_GUMdSAmq8L2KuTaHNozh28CQyU5mlKiCyLnBwBEtaH9eFrBH1DOeKcocbn65RK7RVzFuMM06Mz_sySjlvD5ra0POAwfNDmjCfUS7otnmolg/s400/Law+of+sines+derivation.JPG

WPP#12 Unit:O Concept:10

PROBLEM:Mammoth Mountain Running Camp

A)Segerstrom Cross country team heads over to Mammoth lakes over summer for elevation training. On the first day they do a run called the rock which is 1180 feet up vertically. They stand from the bottom up to the top of the mountain  at angle of 37 degrees. how long up is the trail? 

B) After they arrive at the top of the mountain they look down at an angle of depression of 16 degrees to a houses 3000 feet down vertically. How long is the trail now?

PICTURE:Mammoth Mountain Running Camp

http://www.liftopia.com/ski-resort-info/images/full/619002_logo_1384823487.jpg

Solution:Mammoth Mountain Running Camp

Sources:

http://www.liftopia.com/ski-resort-info/images/full/619002_logo_1384823487.jpg

I/D #2 Unit O-How can we derive the patterns for our special right triangles?

Inquiry Activity Summary

45-45-90 Triangle

First, I cut the square diagonally. I labeled all the angles 90 and the ones who got cut in half 45. 

They all add up to 360 like a square should.Each side length is 1 so we label each side one. ( Step one 

Picture) The diagonal side we don't know yet but since we know two sides are one as stated in the 

directions, we can figure out the diagonal side by using the pythagorean theorem, a^2 + b^2 = c^2. so 

its 1+1=c^2 so then c=sqaureroot 2. (Step two picture) Why "n"? In the sss packet we were given a 45-

45-90 triangle with side lengths of n,n, and n rad 2. Why is that? N is being used as a variable so that it 

can work in all problems with different types of numbers. In this example to get n,n, and nrad2, i just 

multiplied each by n.(Step 3 picture)

30-60-90 Triangle

First , I cut the equilateral triangle straight down the middle. Then I labeled each side and angle 

according to what i was given. Since each side was one and the bottom got cut in half, it is now 1/2. 

We now know 2 sides. One side is 1/2 and one side is 1. We can use the Pythagorean Theorem to 

figure it out but this time we know a and c and are looking for b. (Math work on picture)Finally since 

we now know b is  rad 3/2 and a is 1/2 and c is 1 we need to derive them so that they corresponds to 

all numbers. So what i did was i multiplied each one by 2n. A which was 1/2 became n, b which was 1 

became 2n, and c which was rad 3/2 became n rad 3. (Math work shown on picture). The reason why 

we need to have n is because not all problems will have 1 as the numbers, it has to be able to work for 

all numbers so n acts as the variable.

Inquiry Activity Reflection

Something I never notcied before about special right traingles are that they actaully originate from something. I didn't know that the 45-45-90 came from a sqaure or that the 30-60-90 came from another traingle. I thought that these triangles were just traingles.

Being able to derive these patterns myself aids in my learning beacuse once I know how to get the varaibles that go with these traingles, solving for the sides will be easier now that I know how to get them in the first place. Solving these traingles is no longer just memorization but application of math.

I/D# 1 Unit: N Concept: How do SRT and UC relate?

Inquiry Activity Summary

http://31.media.tumblr.com/tumblr_kueutly2bF1qa3sx1o1_500.gif

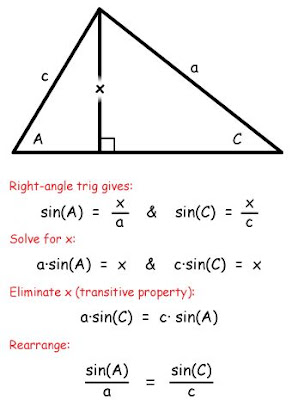
1.First off, i was given a 30' triangle and asked to follow certain steps. First, I  had to label according to the rules of special right triangles. I had a 30' acute angle  which then a 60' and 90' came to add up to 180'. The hypotenuse was 2x, and then the 30' side was xrad3 and the y side was x. The next step told us to simplify all sides so that the hypotenuse was equal to 1. You divide every side by 2x and you get 1,rad3/2, and 1/2. The next steps told us to label the hypotenuse r, the horizontal side x and the vertical side y. I then drew a coordinate plane so that the triangle laid in the first quadrant of the unit circle. I had to label the vertices of the triangle as ordered pairs. They were (0,0), (rad3/2,0), and (rad3/2 ,1/2).

2. Next, we moved on to the 45' 45' 90' triangle which is isosceles. We had to label again according to the rules of special right triangles. We had to simplify all sides so that r was 1. In this case the hypotenuse was xrad2 so we had to divide by xrad2. The x side was x so we divided by xrad 2 and got rad2/2 after we rationalized it. and the y side x also so we got rad2/2 after being rationalized. After we labeled the hypotenuse r and the horizontal side x and vertical side y. Then we drew a coordinate plane so that this triangle was in the first quadrant of the unit circle. Finally we labeled all three vertices of each triangle as ordered pair. They were (0,0), (rad2/2 , 0) , and (rad2/2, rad2/2).

3. Finally, we had to label a 60' triangle. We identified it with the rules of special right triangle. The other side is 30 and we have a 90 degree right triangle. Next we had to simplify the sides so that the hypotenuse was 1. The hypotenuse was 2x to begin with so in order to simplify it to 1 we had to divide by 2x. The horizontal side was x so when I divided it by 2x i got 1/2. The vertical side was xrad3 so dividing it by 2x left me with rad3/2.I then labeled the hypotenuse r and the horizontal side x and vertical side y. I drew a coordinate plane so that the triangle was in quadrant one of the unit circle. Finally i labeled all three vertices of the triangle as ordered pair. They were (0,0) , (1/2, 0) , (1/2 , rad3/2).

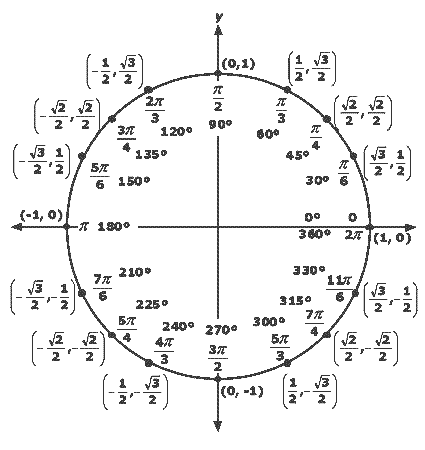
4.This activity helped me derive the unit circle because these three triangles lie in the first quadrant of the unit circle. I had known about the unit circle and the values ( rad3/2 , 1/2) (rad2/2 , rad2/2), and (1/2, rad3/2) were taught to me and i was given no reason for why or how they came about. I was simply told to memorize these values. This activity explained to me and showed me where these values came from. Step two was the part that did the most explaining because simplifying the values showed me where the r , x and y, values came from. Step 6 illustrated to me where these values and triangles fit in the unit circle. Knowing how these values are brought about and how they fit into the first quadrant of the unit circle helped me find reference angles and other values on the other quadrants of the unit circle. Knowing the first quadrant helped me fill out the rest of the unit circle without much work. Simply memorizing and knowing the first quadrant allowed me to fill out and understand the following concepts of this unit as well as future and past concepts. This activity was more like the glue of this unit, it brought everything together.

5.The triangles in this activity lie in quadrant one. Since all the signs are positive because it lies in the first quadrants, all the ordered pairs are positive as well. Remember that All Students Take Calculus!!! As we move into the second quadrant, the only the values that are positive are sine and cosecant values, so all the X values of each ordered pair is negative.  The 30 reference angle is 150. The 60 reference angle is 120. The 45 degree reference angle is 135.As we move into the third quadrant, the only values that are positive are tangent and cotangent so both values of each ordered pair are negative.  The 60 reference angle is 240. The 45 reference angle is 225. The 30 reference angle is 210.The last quadrant the only values that are positive are cosine and secant so the Y of each ordered pair is negative. The 30 reference angle is 330. The 45 reference angle is 315. The 60 reference angle is 300. Their ordered pairs stay the same however the signs of certain values change as we move around the unit circle. As the 60 degree traingle moves around the unit circel you can see the location of the 1 and rad3/2 and 1/2 change as it moves around. The angles also get bigger. The same can be said for the 45 degree trainlge and the 30 degree traingle their r,x, and y values all change locations as it moves around but you can see they are used ass the refernce angles for all around the angle. Knowing these angles helps label them all around. In essance the whole unit circel is 4 30 degree trainlges, 4 60 degree traingles, and 4 30 degree traingles but just flipped around as it goes around.

60 degree traingle
https://blogger.googleusercontent.com/img/proxy/AVvXsEg3l4inVZ2EA6LAuMtER4DPqHRdCxYPCuA2wEoM3f185eKvMawkwg-1V9V7-XVTUIUHua2i5Fw5U0jppuCmhm8TYrFkXILc1SZDaDWFQ_NLtNgVyQ0vaQxf1viwRrvJcjGnqLHrbzEcpiZMkpf7XPbu9SpeUZaWW80VeagxihtbpZfTPfJE3iwUu_-reG2D4dS7CIObgBkotEoL=
=blogger&gadget=a&rewriteMime=image%2F*

60 degree traingles
https://blogger.googleusercontent.com/img/proxy/AVvXsEj6I1JOq4IgpoPFhz57-9nyXOU65aUiAgxvEdSwkP_vDWBUksFc0hs9-wb7lyz53gjovCKxdXRP-boO9FWREf9_AGe041kW2cRSfHYZW8EXyMB9FJ6uKM-kwp93ygFP59HGmYKeC8yFj3DPgpORWxUxsccjqAmK5vfgbhVE0HIrkQy1UXN-dCqK4KNyvhLztTGcbCsvZBWQETGJ=
&gadget=a&rewriteMime=image%2F*

30 degree traingles
http://01.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_34.gif

45 degree traingle
http://01.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_45.gif

45 degree traingles
http://02.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_46.gif

THE COOLEST THING I LEARNED FROM THE ACTIVITY WAS that the unit circle actually derived from something.Last year we were just told what the values were , given them, and told to memorize the unit circle under 5 minutes without further explanation as to why we needed to know it or what it helped us in math.

THIS ACTIVITY WILL HELP ME IN THIS UNIT because once I know the first quadrant and the angles and what comes with them, then the units and points, etc, will come easily. For example, knowing reference angles and co-terminal angles help with future and past concepts. 

SOMETHING I NEVER REALIZED ABOUT SPECIAL RIGHT TRIANGLES AND THE UNIT CIRCLE is that everything I have done with the triangles in the my high school years has finally all come together and made sans. All I learned was for a reason and simply not to memorize useless material.Once I knew the unit circle, the rest of the unit circle came easy. A ll i needed to know was in the first quadrant and then this and future concepts correlated with this.

YAY FOR MRS. KIRCH AND HER EXPLANATIONS OF THE UNIT CIRCLE!!!!:)

Sources:

http://31.media.tumblr.com/tumblr_kueutly2bF1qa3sx1o1_500.gif

http://02.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_46.gif

http://01.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_45.gif

http://01.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_34.gif

https://blogger.googleusercontent.com/img/proxy/AVvXsEj6I1JOq4IgpoPFhz57-9nyXOU65aUiAgxvEdSwkP_vDWBUksFc0hs9-wb7lyz53gjovCKxdXRP-boO9FWREf9_AGe041kW2cRSfHYZW8EXyMB9FJ6uKM-kwp93ygFP59HGmYKeC8yFj3DPgpORWxUxsccjqAmK5vfgbhVE0HIrkQy1UXN-dCqK4KNyvhLztTGcbCsvZBWQETGJ=
&gadget=a&rewriteMime=image%2F*

https://blogger.googleusercontent.com/img/proxy/AVvXsEg3l4inVZ2EA6LAuMtER4DPqHRdCxYPCuA2wEoM3f185eKvMawkwg-1V9V7-XVTUIUHua2i5Fw5U0jppuCmhm8TYrFkXILc1SZDaDWFQ_NLtNgVyQ0vaQxf1viwRrvJcjGnqLHrbzEcpiZMkpf7XPbu9SpeUZaWW80VeagxihtbpZfTPfJE3iwUu_-reG2D4dS7CIObgBkotEoL=

=blogger&gadget=a&rewriteMime=image%2F*

RWA: #1 Unit M Concepts 4-6

Ellipse

1. Mathmatical Definiton : "Set of all points such that the sum of the distance from two points is a constant." (Kirch)
2.  Algebraically defined: An ellipse can either be "fat" or "skinny". The eqaution for a fat graph is  (x-h)^2/a^2 +  (y-k)^2/b^2 =1, the bigger number "a" being on the bottom of x. If the graph is skinny then the eqaution of the graph is (x-h)^2/b^2 +  (y-k)^2/a^2 =1, the bigger number  "a" being below the y in this instance. In the eqaution, the If the bigger number is under the x thwn the graph is going to be fat and if the bigger number is under the y then the graph is going to be skinny. The center is (h,k). H always goes with x and K always goes with y.( Kirch) A skinny graph is going to have a vertical major axis, the axis which the foci lie on, therefore it will be x= #. A fat graph's major axis is going to have a horizontal major axis so it will be y=#. To find the veticies, co-vertices, and foci, you must first know what a,b, and c stand for. A be be derived from the standard eqaution. A being the biggest number and then the sqaure root being taken from it . B then being the second number . To find c , you must use the eqaution a^2-b^2=c^2 following the rule that a >b.(kirch) 

https://images-blogger-opensocial.googleusercontent.com/gadgets/proxy?url=http%253A%252F%252Fformula.algebra.com%252Fcgi-bin%252Fplot-formula.mpl%253Fexpression%253D%252528x-h%252529%25255E2%25252Fb%25255E2%252
B%252B%2B%2528y-k%2529%255E2%252Fa%255E2%2B%3D%2B1%26x%3D0003&container=
blogger&gadget=a&rewriteMime=image%2F 

http://formula.algebra.com/cgi-bin/plot-formula.mpl?expression=%28x-h%29%5E2%2Fa%5E2+%2B+%28y-
k%29%5E2%2Fb%5E2+=+1&x=0003




Eccentricty is a measure  of how much the conic section deviates from being circular.(e=c/a) The ecccentricty of an ellipse must fall in the range of 0<e<1. To find the verticies, you must know the major axis. If the major axis is y=# then the term in the verticie that WILL NOT change will be the y term. However if the major axis is x=# then the term that will not change is the x term. To find the number that changes you must use the center . For example if the number is 5 and the term either a or b is 3 then you go up and down by 3 to get the number.  

The eccentricity of the graph determines how far away the ellipse deviates from being a circle. "An ellipse is defined in part by the location of the foci. However if you have an ellipse with known major and minor axis lengths, you can find the location of the foci using the formula below. The major and minor axis lengths are the width and height of the ellipse."(http://www.mathopenref.com/ellipsefoci.html) The foci will determine how far the ellipse deviates from being a circle since the eccentricty reqauires the use of "c",foci, divided by a.

3. REAL WORLD APPLICATIONS

https://images-blogger-opensocial.googleusercontent.com/gadgets/proxy?url=http%253A%252F%252Fupload.wikimedia.org%252Fwikipedia%252Fcommons%252
Fthumb%2F6%2F65%2FEllipse_Properties_of_Directrix_and_String_Construction.svg%2F411px-Ellipse_Properties_of_Directrix_and_String_Construction.svg.png&container=blogger&gadget=a&rewriteMime=image%2F*

The image displays how the distance from one point to another along the focus is the same all around ,such that it is a constant. It also displays the features of the graph and how it looks like. The foci on the major axis, the minor axis, and how to find the eccentricity.

  Math is indeed fun! The website explains ellipses and provides information about the conic section.
EXTREMELY AMAZING WEBSITE ------>http://www.mathsisfun.com/geometry/ellipse.html

  The video shows everything you would ever want to know about graphing ellipses and all the essential parts.
VIDEO HERE !!! ---------->http://www.youtube.com/watch?v=lvAYFUIEpFI

https://blogger.googleusercontent.com/img/proxy/AVvXsEh5h8peeuMDBHH8DVRZlR64Ik1UAuW61TCpu_yXnwzomn7rIPFgf-paPJe4B_k2CWt9YcFBn0wvP5hNLDrknjrGfuspZh889Ch3LzXBI8iQUT3p5tf_uPzSHUTSG2HZ1-JIHYP2UPzmLSBxpCsCx6-2rJU0hwNSIeRkdY98my0=
.png&container=blogger&gadget=a&rewriteMime=image%2F*

https://blogger.googleusercontent.com/img/proxy/AVvXsEhdFhpdGa65fdHHr0mTtDxzgNlURzeKWspsUScSARuOjWZ3o8RUHQX_paLd3-UZp0xKmhv64D66wVSV51oWdCDJ_XD6jjZdq-23xcgG74hdekqbSKDpq2rSm_ekHXZPi11bvlTUwLlDPzifO-0D8QRXWULYZSU=

This image basically just shows the features of the graph and how two lines from the focus are the same all around. It provides the eqaution to find the graph and "c". 

In the image it illustrates a real life example of a conic section. The distance around the conic from the foci is the same all around. In real life, the ellipse the most occuring "curve" seen beacuse the circle seen from an angle, is an ellipse(http://britton.disted.camosun.bc.ca/jbconics.htm) The reason why ellipses are the most common conic seen is because a circle veiwed a certain way is a ellipse. For example a tilted glass of water is an ellipse.Any cylinder sliced at an angle is also an ellipse. Each planet moves around the sun in an elliptical movement.

4. SITATIONS  http://upload.wikimedia.org/wikipedia/commons/thumb/6/65/Ellipse_Properties_of_Directrix_and_String_Construction.svg/411px-Ellipse_Properties_of_Directrix_and_String_Construction.svg.png

http://www.physics.unlv.edu/~jeffery/astro/ellipse/ellipse_001.png

http://www.youtube.com/watch?v=lvAYFUIEpFI

http://www.mathsisfun.com/geometry/ellipse.html

http://britton.disted.camosun.bc.ca/elliplanet_lg.JPG

http://www.mathopenref.com/ellipsefoci.html

http://en.wikipedia.org/wiki/Eccentricity_(mathematics)

http://britton.disted.camosun.bc.ca/jbconics.htm

http://formula.algebra.com/cgi-bin/plot-formula.mpl?expression=%28x-h%29%5E2%2Fa%5E2+%2B+%28y-k%29%5E2%2Fb%5E2+=+1&x=0003